For loop solution

When I first wrote up this problem I didn’t know about the Vectorize function so I wrote it as a for loop. I think some are more comfortable with that kind of solution, so I’m going to present it for comparison purposes:

equil_frac_loop <- function(Ta, verbose = FALSE){
  frac_factor <- numeric()
  for(i in 1:length(Ta)) {
    if(Ta[i] > 100 & verbose) {
      warning(paste('Temperature values are outside the bounds of the method -',
        'may generate anamolous data.'))
    }
    temp_K <- Ta[i] + 273.15 #Convert C to K
    if(Ta[i] >= 0) {
      frac_factor[i] <-  warm(temp_K)
    } else if(Ta[i] < 0) {
      frac_factor[i] <-  cold(temp_K)
    } else {
      stop("Something's wrong with your temperature values.")
    }
  }
  frac_factor
}

Vectorized solution

To generate the vectorized solution, we first write the unvectorized “skeleton” to our problem:

equil_frac_unvec <- function(Ta, verbose = FALSE){
  if(Ta > 100 & verbose) {
    warning(paste('Temperature values are outside the bounds of the method -',
      'may generate anamolous data.'))
  }
  temp_K <- Ta + 273.15 #Convert C to K
  if(Ta >= 0) {
    return(warm(temp_K))
  } else if(Ta < 0) {
    return(cold(temp_K))
  } else {
    stop("Something's wrong with your temperature values.")
  }
}

Now, here is where the magic happens. To vectorize the above function, all we need to do is wrap it with Vectorize and save it as a new object.

equil_frac_vec <- Vectorize(equil_frac_unvec)

And that’s it! Our unvectorized function is now vectorized. But do the for loop and vectorized forms generate the same solution? Let’s check the outputs with the all.equal function, which for a numeric vector, will check that each element in a “target” and “current” vector are the same.

#First let's generate some "temperatures".
temperatures <- runif(n = 20, min = -30, max = 30)
#Apply the two solutions.
vec_out <- equil_frac_vec(Ta = temperatures)
loop_out <- equil_frac_loop(Ta = temperatures)
#Test if they are equivalent; this will return TRUE if all values are the same.
all.equal(loop_out, vec_out)

## [1] TRUE

Well, look at that! all.equal returned TRUE, meaning both methods produced the same results.

Benchmarking

This first bit of code just tells bench which functions to run and how many times.

vector_compare <- bench::mark(
  `Apply family` = sapply(temperatures, equil_frac_unvec),
  `Purrr family` = map_dbl(temperatures, equil_frac_unvec),
  `Vectorize` = equil_frac_vec(temperatures),
  `For loop` = equil_frac_loop(temperatures),
  iterations = 10000
)

Eazy peazy! So, what do the results look like (after removing some things that we don’t care as much about for the purposes of this post)?

vector_compare %>%
  select(expression, min, median, `itr/sec`, mem_alloc, total_time) %>%
  arrange(median) %>%
  mutate(expression = names(expression))

## # A tibble: 4 x 5
##   expression        min   median `itr/sec` mem_alloc
##   <chr>        <bch:tm> <bch:tm>     <dbl> <bch:byt>
## 1 For loop       27.6us   32.1us    28704.      792B
## 2 Apply family   47.4us   53.3us    17074.      720B
## 3 Purrr family   50.9us   57.3us    16686.    4.23KB
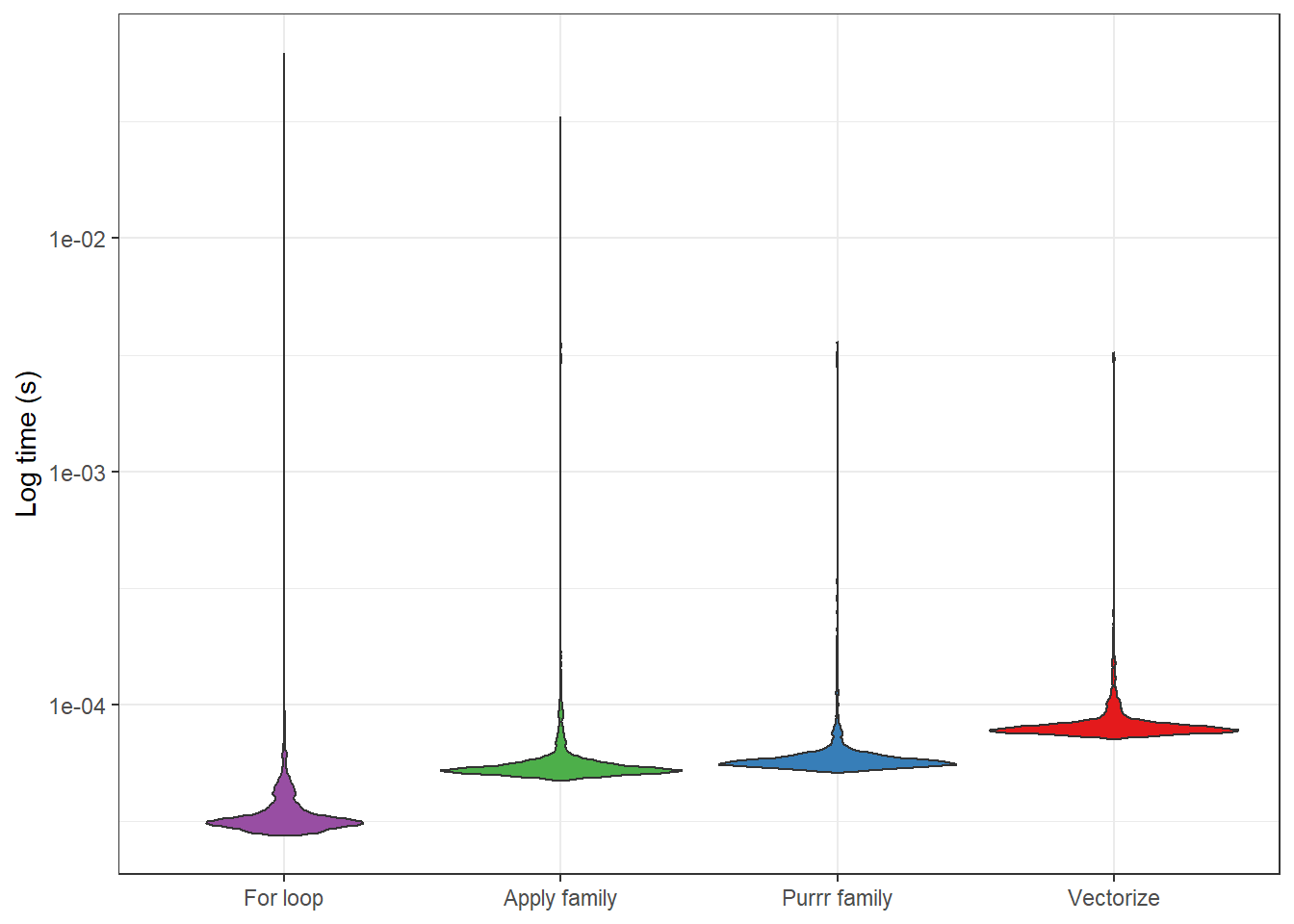
## 4 Vectorize      71.3us   79.6us    11917.      720B

Fascinating! It looks like the for loop function was fastest, while the vectorize function was slowest. Relatively, the for loop function was ~ 2 times faster than the vectorize function, on average (median).

But how do the results look? The image below provides some indication. It looks like the distributions of the processing times are pretty scattered (hence the need to log the scale), but the medians appear fairly representative. This, then, suggests that it is really the for loop function we’d want to use, if performance became a big issue. Or, given my exploration of Rcpp, we might want to consider writing the function in C++. But we’d need to run the code a lot to justify the work required for these alternative strategies.

vector_compare %>%
  unnest(cols = c(time, gc)) %>%
  select(expression, time, median) %>%
  arrange(median) %>%
  mutate(expression = fct_inorder(expression)) %>%
  mutate(time = as.numeric(time)) %>%
  ggplot(aes(expression, time, fill = expression)) +
  geom_violin(show.legend = FALSE) +
  labs(x = NULL,
    y = "Log time (s)") +
  scale_y_log10() +
  theme_bw() +
  scale_fill_brewer(palette = "Set1", direction = -1)

For more on Vectorize, check out this post by Dean Attali.

Vectorize as a function factory

I mentioned earlier that Vectorize is taking advantage of R’s functional programming infrastructure. But how is it doing that? Well, that’s a bit beyond the scope of this post, but I do think it interesting to see what the internals of our new vectorized function look like:

equil_frac_vec

## function (Ta, verbose = FALSE) 
## {
##     args <- lapply(as.list(match.call())[-1L], eval, parent.frame())
##     names <- if (is.null(names(args))) 
##         character(length(args))
##     else names(args)
##     dovec <- names %in% vectorize.args
##     do.call("mapply", c(FUN = FUN, args[dovec], MoreArgs = list(args[!dovec]), 
##         SIMPLIFY = SIMPLIFY, USE.NAMES = USE.NAMES))
## }
## <environment: 0x0000000015b5d288>

That looks nothing like my original code! So something really fascinating is going on to turn the unvectorized function into that crazy set of lines above. But I’ll leave the exploration of that process for another post.

Other ways of applying conditions in R

Since we’re talking about conditionals, I thought it worth mentioning two other useful ways for applying conditions to a vector or other object: base::switch and dplyr::case_when. These are great for “unnesting” complicated control flows, making code easier to read, understand, and write. Worth checking out.